On Monday the 2012 Nobel Memorial Prize in Economic Science was awarded to Lloyd Shapley and Al Roth, for their work on market design and matching theory, which relate to how individuals and firms find and select one another in areas from school choice to jobs to organ donations to marriage itself.
Dr. Shapley, 89, a professor emeritus at UCLA, made early theoretical contributions to the topic in the 1950’s and 1960’s.
Al Roth, in the process of moving from Harvard to Stanford, working independently, put the theories to practical use in markets including assigning students to public schools in New York, Boston, Chicago, and Denver, matching kidney donors and, importantly, matching new doctors to hospitals.
Why is the work so noteworthy?
Disclosure time: I consider Al a friend, and have corresponded with him in the past about his work and its applicability to other contexts including Law Land. In fact, after the Nobel announcement, I sent him a congratulatory email which I fully expected to be buried in an avalanche of similar emails, phone calls, and media requests, all from more exalted folks. Al responded to me in less than five minutes. That’s Al.
These markets have an unusual feature in common: There are no prices, which normally do the heavy lifting of resource allocation and matching up buyers and sellers. Absent prices, how do you design a market that can arrive at a stable and optimal outcome?
And is it possible to arrive at a stable outcome even when persons on either side of the market disagree about what qualities make for the right match?
Turns out that it is possible, and that systems can be designed that produce matches that:
- are fair;
- are “stable” in the strict sense that no one in any of the resulting matches would want, and be able, to break off and pair up with a counterparty in another match;
- and that cannot be manipulated by sophisticated players to their advantage.
Here’s how it works in a nutshell, courtesy of the NYT’s story on the Nobel:
In older matching systems, a student would apply to his first-choice school, which was often popular. If the student did not get in, then the application would be sent on to the student’s second choice. But if that was also a popular choice, then that school’s program would have already filled up by the time his application was even considered, and the process would repeat itself with his third-choice school and so on.
Even if students were qualified to get into one of their top schools, they could be shut out because they did not rank their preferences strategically. This created an incentive to try to game the system by listing a less popular school as their first choice because that way they would at least have a chance of getting in somewhere.
Mr. Roth designed a system in which students had an incentive to tell the truth about where they wanted to go. A centralized office could then assign them to a school best suited for them, based both on their own preferences and the preferences of the schools they were applying to.
The school systems he helped create use a “deferred acceptance algorithm,” which was developed by Mr. Shapley’s theoretical work.
The system works by tentatively accepting students to their top-choice school. It holds off on the final assignment until it has gone through all the other applications to make sure there are not other students who have a higher claim to a spot at that given school (because of higher test scores, a sibling at the school or whatever other criteria the school prioritizes), even if those students happened to rank the school lower on their list of preferences.
“The idea is to level the playing field,” Mr. Pathak said. “You want to make sure that not only do sophisticated players not have to spend the time learning the strategies and different heuristics that will get them ahead, but also that unsophisticated players are not hurt by the fact that they are not aware of all this information.”
This same sort of system is used to match new medical school graduates to medical residency programs, which was once a messy process that led to a lot of unhappy candidates. Now all residency assignments are posted simultaneously. In the mid-1990s Mr. Roth redesigned the system to help match married couples who were jointly looking for jobs at hospitals.
Does it really work?
Let’s get specific.
Before the New York City school system intervention by Al, the more sophisticated students and their families could “game” the system by strategically misrepresenting their preferences, and fully one-third of students ended up paired with a school they had not expressed a preference for at all. After Al’s system was introduced, participation rates climbed to near universality, the opportunity for strategic gaming disappeared (stated otherwise, the dominant strategy was to state one’s true preferences), and the number of students unmatched with a preferred school dropped to about 3% (they were then handled administratively). Needless to say, the system remains in place.
How about matching medical students with hospital residency opportunities? If this sounds like matching law students with law firms, it should.
Nearly three years ago, Prof. Ashish Nanda at Harvard Law School wrote History Rhymes, which proposed adopting a similar matching algorithm to pair students and firms in Law Land.
What problem was the medical matching system supposed to solve? Actually, the way the medical student/hospital recruiting market used to work was remarkably parallel to how the law student/law firm recruiting market works today: There was a terribly powerful dynamic pushing all involved to be “first:”
- Hospitals wanted to interview the “best” medical students first;
- Medical students wanted to interview the “best” hospitals first; and
- Medical schools wanted their students to be interviewed first.
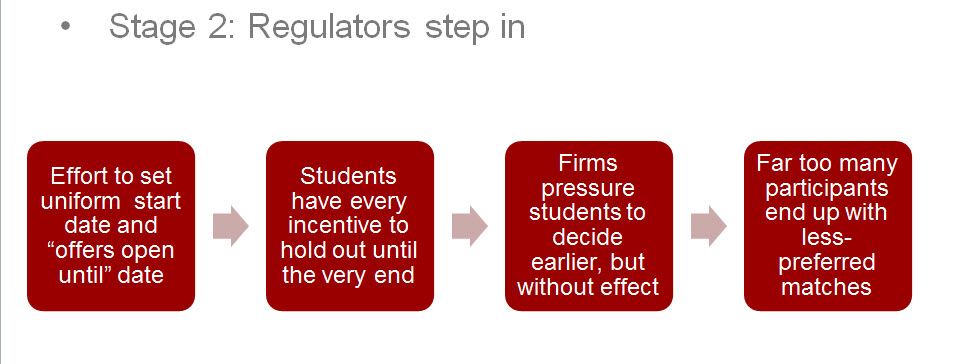
It reached the point, right after World War II, that hospitals were sending out offers to medical students two years in advance of their residency by telegram at midnight on a certain day and students were required to respond by telegram, by noon that same day.
Quaint technology aside, sound familiar?
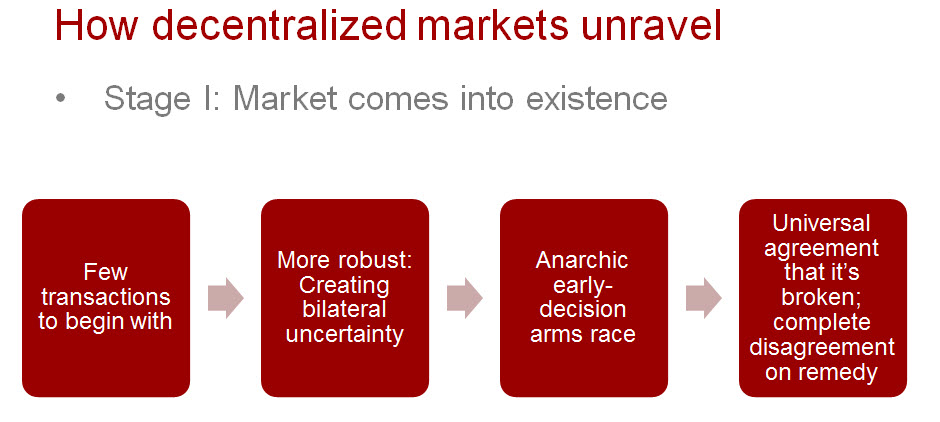
Key is to understand that no one involved really enjoyed, desired, or even benefited from this market dynamic. But each individual participant was pursuing what seemed in their best individual self interest. What everyone ends up with, however, is one enormous negative-sum arms race. Everyone is actually worse off, after great expenditures of money and anxiety.
One of the primary sources of systemic market breakdown such as this is that the market is decentralized. Thanks to Al and others, the toxicology of decentralized markets is now much better understood. It goes like this (click to enlarge any image–opens in new window):
Again, is a centralized market really the answer? Here’s the data:
- The medical student matching system (technically, the “National Resident Matching Program”) has endured for over 60 years
- 37,556 applicants
- 4,176 employers
- 25,520 matches (2010 figures)
- The National Bureau of Economic Research found over 100 markets organized with a central clearinghouse, only three of which had abandoned the clearing system (and found that all three were due to sui generis exogenous factors—indeed, the paper is titled, The Collapse of a Medical Labor Clearinghouse—And Why Such Failures Are Rare)
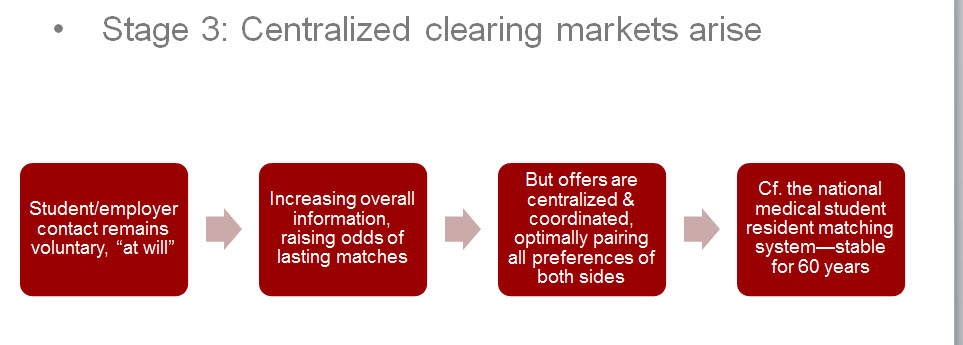
A bit more on how the “NRMP” works: After students and hospitals get to know each other through free market, bilateral searches by students for residency programs and by hospitals for candidates—followed by mutually agreed meetings and interviews—students enter their rank-ordered list of preferred hospitals into the matching system and hospitals do the same with their preferred lists of students.
On a single “Match Day” each year, typically in March, the algorithm runs. Students learn which hospital they’re going to and hospitals learn which students they’re getting.
Need the match be mandatory?
In some cases, actually, it’s not; for example, an experimental program being developed in Pennsylvania to recommend matches between foster parents and adoptive children will leave the final decision to the parents and social workers. But it’s a tremendous advance from complete dysfunction and chaos.
In the case of the (mandatory) NRMP, because the resulting matches are optimal and “stable” in the rigorous sense described above, the system has endured in concept (technology has of course evolved) since the day it was implemented after World War II.
And why shouldn’t centralized matching yield a stable, equilibrium solution for these previously dysfunctional markets? They’re merely benefiting from Nobel Prize winning insights.